where L*M_t is the amount of thermal energy that would be lost if evaporation were the only way of loosing heat. In other words M_t*L is nothing else but electric energy, E_o, measured at the same time as M_o. In other words, Q_c = E_o - L*M _o and excess heat, H, is given by:

H = Q_v + Q_c - E_o = L*(Mp - M_o)+ (E_p - E_o) . . . . . . . . (5)

Note that excess heat becimes L*(M_p-M_o) when E_p and E_o are identical. This relation is intuitively obvious without the derivation. Nuances involved in experimental determinations of H will be addressed in the next section. The equation (1) is certainly satisfied when an ohmic resistor is used to sustain boiling. But will it also be satisfied when boiling takes place during the high voltage electrolysis? That is the question we want to answer.

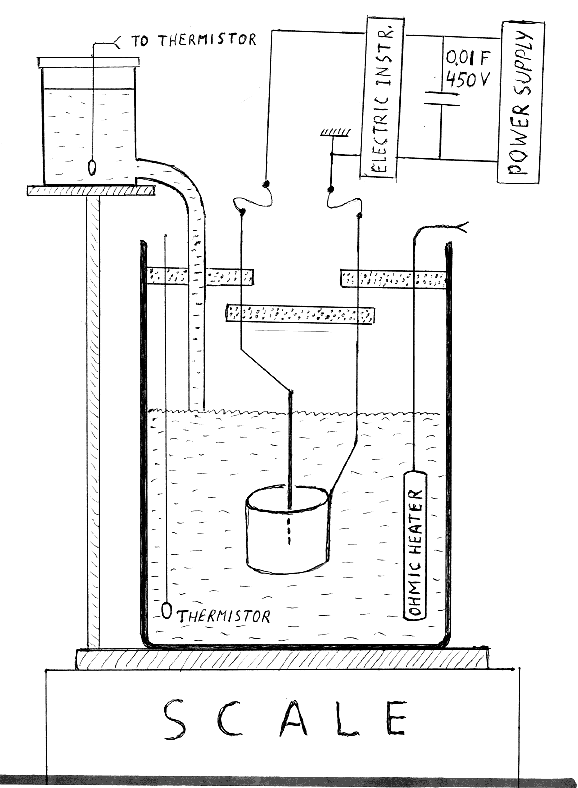
FIGURE 1
Schematic diagram of our first setup. The volume of the electrolyte was 650 cubic centimeters. The dotted baffles, in the upper section of the cell, offer an escape path to the vapor but not to the splashing electrolyte. Vertical rods supporting the electrodes are mounted on these baffles. The “electrical instruments” box, at the upper right corner, stands for the Clark-Hess meter (model 3200). It is essentially a set of three digital instruments: an ammeter, a voltmeter and a wattmeter.
= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

Masses of water evaporated in consecutive tests (M_p and M_o were determined from the readings of the scale. Light flexible filaments were used to connect electrical components inside the vessel with outside circuits. That arrangement did not prevent us from measuring mass differences (typically 40 grams) with a sufficient accuracy (at least 0.5%). The entire vessel was wrapped in a layer of polyethylene foam. The purpose of that thermal isolation was to keep the walls temperature as high as possible in order to minimize condensation of vapors on the inner surface. Condensed water dripping back into the electrolyte would reduce values of m1 and M_o . Splashing, on the other hand, would make M_p and M_o larger than what were evaporated.

Note that the intensity of splashing, if not mechanically reduced, would increase with the applied voltage. This could possibly create an illusion of a voltage-dependent excess heat. The same kind of illusion could occur if the “invisible splashing” was significant. Ideally only water vapor (plus some hydrogen and oxygen) should escape from the electrolyte. Suspecting that tiny droplets of electrolyte might also be escaping from the cell we compared concentrations of the electrolyte before and after some tests. These two concentrations should be the same because evaporated water is replaced by fresh water. But replacing droplets of the electrolyte with water would make the second concentration smaller than the first. A reduction of the concentration was noticeable but not significant to create an illusion of excess heat. Another possibility of a systematic error, could possibly occur if the rising temperature of water in the reservoir were not taken under consideration. The flow of steam escaping from the vessel increases with voltage and affects the temperature in the reservoir. This, in turn, changes the value of L used in formulas 3 and 4. Using L=2595 (correct at 20 C) when in reality it is 2427 (at 40 C), for example, would create an illusion that Qv and Qc are 7% higher.

The ohmic heater was used to preheat the electrolyte to the boiling temperature and to measure M_o. After that the ohmic heater was turned off and boiling was maintained by the current flowing through the electrolyte. The evaporated masses m1 were measured after the ohmic heater was turned off and after desired voltages were applied between the anode and the cathode. The Figure 2 shows time dependencies of our two most essential parameters. The line labeled “masses” refers to evaporated water (M_p or M_o in grams along the left-vertical axis). Likewise, the line labeled “energies” refers integrated electric energy (E in kJ along the right-vertical axis). Other measured, or computer-calculated, parameters were also monitored during the experiments but their time dependencies are not shown in the figure below. The mass lost was essentially zero until the boiling temperature was reached. After that the amount of water evaporated started increasing. The segment AB of the mass curve was used to determine M_o. The segments CD and EF of that curve were used to determine M_p at two different voltages. The corresponding segments of the energy curve, A'B', C'D' and E'F' were used to determine the values of the energy received in the matching time intervals.

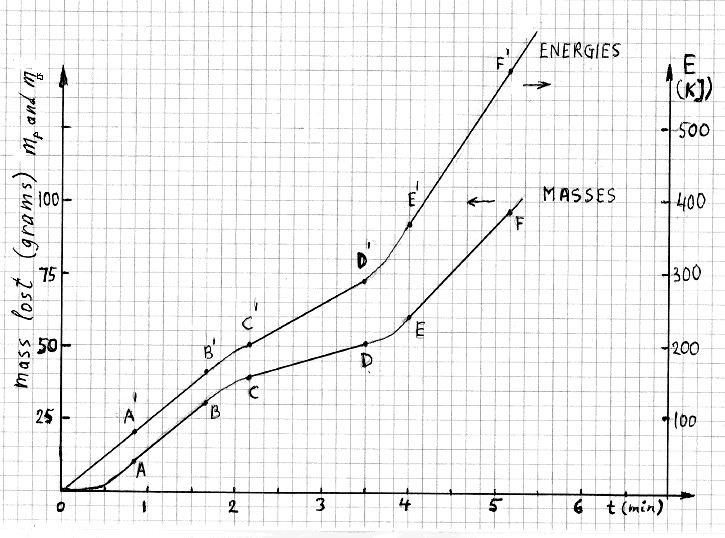
FIGURE 2
Typical time dependencies of M_p (or M_o) and of E for three short tests. Boiling point was reached at t=0.5 min but the first test started (in this hypothetical illustration) at t=0.833 min.

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

Due to micro explosions in the electrolyte, especially in tests above 300 volts, the mass curves often displayed wiggles (not shown in figure 2). Wiggles, representing dynamic effects on the scale, did not interfere with determinations of masses of the evaporated water because only initial and final readings were needed. We were always able to stop cell shaking by lowering the voltage for three to five seconds.

Results

Figure 3 shows how the rates of non evaporative losses (measured with the ohmic heater) depended on the electric power. The values of electric power, in watts, are shown along the horizontal axis while the vertical axis shows rates of non evaporative losses (also in watts). The rate of loosing heat by conduction and convection increases with electric power. This is an expected result; the rising column of steam acts as an air pump which drives convection currents more strongly than when generation of steam is less intense. Furthermore, more rapid boiling is equivalent to more intensive mixing of the electrolyte. This too is likely to increase the rate of cooling by conduction and convection.

The values of E, Q_v and Q_o, at different voltages, are shown in the table below. Most cells of this table contains two numbers; the mean value and the standard deviation. For example, a cell at the intersection of the row labeled 300 V and the column labeled E, shows that the . . .

Single numbers, in the last column, labeled COP, are coefficient of productivity at different voltages. By definition:

COP = (Q_v + Q_c) / E

The numerical values of COP were calculated from the mean values of Q_v, Q_c and E, at corresponding voltages. The data show that . . .

Please revisit this unit in November to see the results.

APPENDIX 1
Measuring electric energy

The electric energy E, delivered to a cell, is the integral (over a test duration) of dE = i(t)*v(t)*dt. The instrument we used, Clark-Hess model 2330 power analyzer, sampled the v(t) and i(t) about 2000 times per second. As expected, the voltage between the cell electrodes, v(t), was essentially constant but the current i(t) was highly irregular. Digitized samples of v(t) and i(t) were recorded by the computer and the cumulative E was displayed during the data acquisition, as shown in Figure 2. A highly irregular nature of the i(t) waveform guarantees random sampling and the average energy, over a time longer than several seconds, is highly reliable. To verify this we also used an a.c. watt meter at the input of our d.c. power supply. The a.c. energy, E', measured with that instrument was only slightly larger than the d.c. energy, E. The difference, (E'-E), was consistent with what is necessary to operate the power supply when it is not loaded. A high quality digital multimeter, Fluke 87, was also used to measure the mean current. The result was identical with the mean current measured by the Clark-Hess instrument.

APPENDIX 2
Measuring electric energy
A polycarbonate cell whose height and internal diameter were . . . cm and .... cm, respectively, replaced the taller cell used in the previous set of experiments. The new cell (see Figure 4) has a lid made from the linen-based phenolic plastic. The lid is firmly attached to the cell with four nylon-tipped screws. The electrodes, the water reservoir, the ohmic heater, and the thermistor are now mounted on the lid. A PVC exhaust pipe, whose inner diameter is 2.54 cm, is also mounted on the lid. Its purpose is to conduct steam escaping into air. A plastic baffle, placed 2 cm below the pipe’s input (inside the cell), is an effective shield against consequences of splashing the electrolyte.

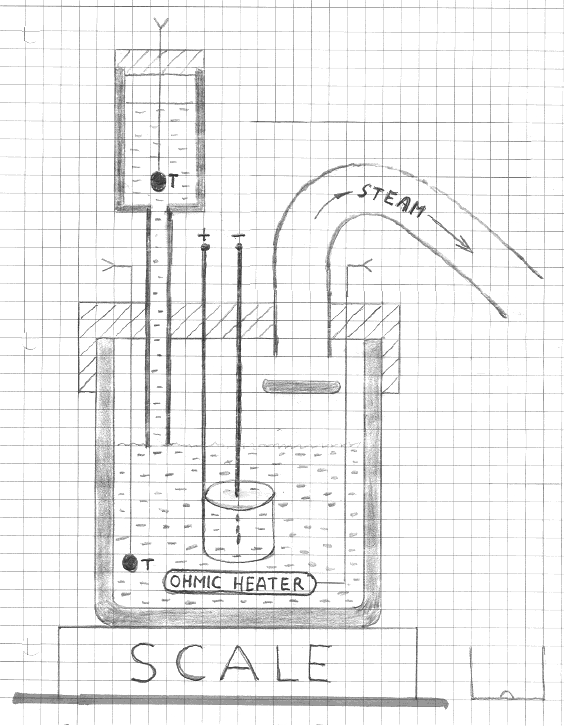
FIGURE 4
Schematic diagram of our second setup.

Some condensation is expected to occur on the inner surface of the exhaust pipe, mostly in the outermost section where the temperature is the lowest. That section was directed downward so that drops of water could drip down to be collected. Note that in a vertical pipe condensed water would return to the electrolyte. Also note that steam ejected from the cell is kept away from the water reservoir and from electrical connections above the lid.

The Pt-coated Ti mesh anode, same as before,is now supported by two titanium rods (instead of one) to minimize shaking. As before, the exposed end of the tungsten cathode (about 1 cm) was located at the center of the cylindrical anode. One of the problems encountered with the previously used cell was arcing between the electrodes in the space above the electrolyte. All metallic components in the new cell are covered with insulation. Hopefully this will reduce the probability of arcing.

NOT TO FORGET:
1) Recognizing that the idea of measuring the concentration of salt in the electrolyte (before versus after a test, in order to investigate a possibility of ejection of tiny droplets) was suggested to us by Dennis Cravens. Also his critical comments on measuring E.
2) Electroplating as a method of calibrating our C-H ammeter, if necessary.
3) Recognizing Clauzon's help in providing details about their setup.
4) Try to understand presence of tungsten in the water reservoir (discovered with the X-ray fluorescence instrument)
5) Recognizing Puthoff's (ETI?) hospitality, contribution and encouragements.
6) ?